maelstRom imprinting tutorial

maelstRom for imprinting analyses

maelstRom includes functionalities for the detection of (differential) imprinting, which were previously published by our lab (Goovaerts et al. (2018)). This extreme form of allele-specific expression (ASE) requires a seperate and robust analysis pipeline, as maelstRom’s beta-binomial mixture models (as introduced in the “maelstRom Allelic Dispersion tutorial”) rely on the occurrence of observeable heterozygosity in RNAseq data to study ASE. The latter is absent in fully imprinted loci, and this will results in e.g. numerical failure during maelstRom’s beta-binomial mixture model fit, or otherwise categorization as a low-quality locus. This vignette covers an analysis pipeline retaining these loci and quantifying their degree of (differential) imprinting.

A toy dataset

This vignette utilizes the same toy dataset as the “maelstRom Allelic Dispersion tutorial”. As such, the code chunk below re-runs the code found there up to and including “Enabling parallellization”; please consult this tutorial for an in-depth explanation of input data collection and pre-processing.

data("maelstRom", package = "maelstRom")

# maelstRom expects lists:
controlList <- list() 
caseList <- list()

for(LOC in unique(ControlCountsToy$Locus)){                 # For every locus...
  interDF <- ControlCountsToy[ControlCountsToy$Locus==LOC,] # extract nucleotide counts,
  controlList[[LOC]] <- interDF                             # and put it into the list
}

for(LOC in unique(CaseCountsToy$Locus)){                    # Do the same for case data
  interDF <- CaseCountsToy[CaseCountsToy$Locus==LOC,]
  caseList[[LOC]] <- interDF
}

for(n in names(controlList)){
  controlList[[n]] <- maelstRom::standard_alleles(controlList[[n]])
} 
#> Warning:
#> replacing
#> previous import
#> 'data.table::yearmon'
#> by
#> 'zoo::yearmon'
#> when loading
#> 'maelstRom'
#> Warning:
#> replacing
#> previous import
#> 'data.table::yearqtr'
#> by
#> 'zoo::yearqtr'
#> when loading
#> 'maelstRom'

for(n in names(caseList)){
  
  interDF <- caseList[[n]]
  interDF$ref_alleles <- controlList[[n]]$ref_alleles[1]
  interDF$ref <- controlList[[n]]$ref[1]
  interDF$var <- controlList[[n]]$var[1]
  interDF$ref_count <- interDF[,which(colnames(interDF)==interDF$ref[1])]
  interDF$var_count <- interDF[,which(colnames(interDF)==interDF$var[1])]
  
  caseList[[n]] <- interDF
  
}

for(n in names(controlList)){
  controlList[[n]] <- maelstRom::prior_filter(controlList[[n]], min_median_cov = 0, 
    min_nr_samples = 20, checkref_filter = FALSE, prior_allelefreq_filter = FALSE, 
    min_PriorAlleleFreq = 0)
  if(is.null(controlList[[n]])){
    # Filter out case data if corresponding control data was removed:
    caseList[[n]] <- NULL 
  }
}


NC <- 1 # Number of Cores, CHANGE THIS for a speed-up when working on a linux machine

NS <- length(controlList) 
spl <- c(0, cumsum(rep(floor(NS/NC),NC)+c(rep(1,NS-floor(NS/NC)*NC),
         rep(0,NC-NS+floor(NS/NC)*NC)))) 
ParCTRL <- vector(mode = "list", length=NC)
for(i in 1:NC){ # Put the split input data into a list for parallellisation
  ParCTRL[[i]] <- controlList[(spl[i]+1):(spl[i+1])]
}
ParCASE <- vector(mode = "list", length=NC)
for(i in 1:NC){ # Put the split input data into a list for parallellisation
  ParCASE[[i]] <- caseList[(spl[i]+1):(spl[i+1])]
}

Metaparameter estimation

Like in the “maelstRom Allelic Dispersion tutorial”, some metaparameters need to be calculated (Sequencing Error, and inbreeding coefficient); the code and explanations here is identical to that tutorial, with the exception that we also update the control data (ParCTRL and controlList) using AllelicMeta_est_par’s output, to include a preliminary per-locus reference allele fraction estimate among the population’s genotypes. This can be used as a prior filter during imprinting detection.

cl <- parallel::makeCluster(getOption("cl.cores", NC))
GenoFinData <- parallel::parLapply(cl, X = ParCTRL, fun = maelstRom::AllelicMeta_est_par,
  MinAllele_filt = 0.15, SE_filt = 0.035, NumSamp_filt = 20, MedianCov_filt = 4)
parallel::stopCluster(cl)

# Update control list with a prior allele frequency estimate:
ParCTRL <- lapply(GenoFinData, `[[`, 1)
controlList <- do.call(c, lapply(GenoFinData, `[[`, 1))

SE_vec <- do.call(c, lapply(GenoFinData, `[[`, 2))
F_vec <- do.call(c, lapply(GenoFinData, `[[`, 3))
SEmedian <- median(SE_vec)
Fmedian <- median(F_vec)
cat(paste0(c(SEmedian, Fmedian), ","))

0.00248190279214063, 0.00872807570598289,

Detecting imprinted and differentially imprinted loci

Imprinting analyses in maelstRom are quite different from the analyses up until now in that they don’t rely on beta-binomial modelling and make different assumptions about the data. They are, generally speaking, a bit more robust because imprinting is usually an extreme phenomenon, i.e. heterozygous samples of imprinted loci will almost always “seem like” homozygous samples because one of the alleles has been silenced almost entirely. Partial imprinting can exist and maelstRom can detect it, but this phenomenon is not modelled as thoroughly as the previous ones in this vignette.

First off we assume samples show no AB and are conform Hardy-Weinberg-Equilibrium while taking imprinting into account, which is tested by symmetry_gof. It does this by assessing whether the number of samples with a reference allele fraction > 0.5 (and so also the number with a fraction <= 0.5) is equal to that expected under HWE assuming no AB using a chi square test. This may seem kind of heuristic at first and prone to fail if there is even a little AB, but remember we want to mainly retain imprinted loci, meaning heterozygous samples should behave as one of both homozygotes (and so clearly feature reference allele fractions > 0.5 or <=0.5) so this filter is very fitting for retaining HWE-conform samples that are at the same time likely to showcase imprinting. A good filter setting is requiring the p-value to be at least 0.05.

After applying these filters, imprinting_est detects imprinted loci in the remaining control samples by first assuming an unshifted binomial mixture model, then splitting up the heterozygous samples in two separate groups according to a degree of imprinting \(i\) and varying this \(i\) from 0 to 1 in a for-loop, calculating likelihoods along the way to perform a likelihood-ratio test to check for differential imprinting (i.e. compare the most likely model with the non-imprinted one; \(i=0\)). For completeness, the imprinted PMF is (see Goovaerts et al. (2018) for a full elaboration):

\[ \small \begin{aligned} \mathrm{PMF}(&counts_{ref}|counts_{total}) = P_{rr} * {\tt pbinom}(x=counts_{ref} \ |\ n=counts_{total}, p=1-SE) \ + \\ & 0.5P_{rv} * {\tt pbinom} \left( x=counts_{ref} \ |\ n=counts_{total}, p=\frac{0.5-\frac{i}{2}}{1-\frac{i}{2}}(1-SE)+\frac{0.5}{1-\frac{i}{2}}SE\right) \ + \\ & 0.5P_{rv} * {\tt pbinom} \left( x=counts_{ref} \ |\ n=counts_{total}, p=\frac{0.5-\frac{i}{2}}{1-\frac{i}{2}}SE+\frac{0.5}{1-\frac{i}{2}}(1-SE)\right) \ + \\ & P_{vv} * {\tt pbinom}(x=counts_{ref} \ |\ n=counts_{total}, p=SE) \end{aligned} \]

After retaining only significantly and sufficiently imprinted loci (5% FDR level, degree of imprinting at least 0.6 and median degree of imprinting at least 0.8 for robustness; see median_imprinting for the latter’s calculation) using the final_filter function, we use LOItest_logreg() to test for differential imprinting. More specifically, logistic regression is used to evaluate whether case samples feature a significantly higher number of apparently heterozygous samples than control samples (by considering the least expressed allele as a success; more details can be found on the function’s help page. Note that the logistic regression approach takes into account variable coverage between samples, contrasting our previously published strategy by Goovaerts et al. (2018)). If this is true, it indicates that a significant fraction of heterozygous samples in tumor tissue “lost their imprinting” and actually started expressing both alleles again. We call these loci “differentially imprinted”, as we reserve the term “loss-of-imprinting” for the phenomenon where differential imprinting co-occurs with increased total expression, indicative of re-expression of the silenced allele. Comments in the code below provide additional insight into the imprinting analysis pipeline:

# Perform filtering using symmetry_gof()
# Notice we use allelefreq_prel as input in this function, which is the allele frequency as 
# estimated by an UNSHIFTED binomial mixture model using AllelicMeta_est() earlier in this 
# vignette, which is what symmetry_GOF assumes as well so it's only fitting.
# We also enforce that this allelefreq_prel can not be more extreme than 0.15 or 0.85, 
# because detecting imprinting would be very hard otherwise.
ImprData <- controlList
for(LOC in names(controlList)){
  if (ImprData[[LOC]]$allelefreq_prel[1] <= 0.15 || 
      ImprData[[LOC]]$allelefreq_prel[1] >= (1 - 0.15)) {
    ImprData[[LOC]] <- NULL
  } else {
    ImprData[[LOC]]$sym <- maelstRom::symmetry_gof(ImprData[[LOC]]$ref_count, 
      ImprData[[LOC]]$var_count, ImprData[[LOC]]$allelefreq_prel[1])
    if (ImprData[[LOC]]$sym[1] <= 0.05) {
      ImprData[[LOC]] <- NULL
    }
  }
}


# Detect imprinted control loci
impr_res <- data.frame()
for(LOC in names(ImprData)){
  i_results <- maelstRom::imprinting_est(ImprData[[LOC]]$ref_count, ImprData[[LOC]]$var_count, 
                allelefreq = ImprData[[LOC]]$allelefreq_prel[1], SE = SEmedian, inbr = Fmedian)
  # An additional robustified "median imprinting" across samples to be used as possible 
  # additional filter criterion:
  med_imp <- maelstRom::median_imprinting(ImprData[[LOC]]$ref_count, ImprData[[LOC]]$var_count, 
              allelefreq = ImprData[[LOC]]$allelefreq_prel[1], inbr = Fmedian)
  results_z <- data.frame("position" = ImprData[[LOC]]$Locus[1], "LRT" = i_results$LRT, 
    "p" = i_results$p_value, "estimated.i" = i_results$est_i, "allele.frequency" = 
    ImprData[[LOC]]$allelefreq_prel[1], "reference" = ImprData[[LOC]]$ref[1], "variant" = 
    ImprData[[LOC]]$var[1], "med_cov" = ImprData[[LOC]]$coverage[1], "nr_samples" = 
    nrow(ImprData[[LOC]]), "GOF" = i_results$GOF_likelihood, "symmetry" = 
    ImprData[[LOC]]$sym[1], "med_impr" = med_imp, stringsAsFactors = FALSE)
  impr_res <- rbind(impr_res, results_z)
}
# Retain significantly imprinted loci (5% FDR) utilizing some additional filters, amongst
# which a custom  Goodness-Of-Fit which more or less corresponds to a locus' likelihood of
# the imprinted model*coverage; 0.8 is a good cutoff. Other filter criteria are imprinting 
# (0.6) and median imprinting (0.8)
impr_res_FIN <- maelstRom::final_filter(data_hash=NULL, impr_res, results_wd=NULL, gof_filt = 0.8, 
  med_impr_filt = 0.8, i_filt = 0.6, adj_p_filt = 0.05, file_all = FALSE, file_impr = FALSE, 
  file_all_counts = FALSE, file_impr_counts = FALSE)


# Amongst actually imprinted loci, detect differential expression in case data
pos_impr <- as.character(impr_res_FIN$position)
p_DI_df <- impr_res_FIN
p_DI_df$DI_pval <- 1
for(LOC in pos_impr){
  CData <- controlList[[LOC]]
  TData <- caseList[[LOC]]
  p_DI <- maelstRom::LOItest_logreg(CData$ref_count, CData$var_count, 
                                  TData$ref_count, TData$var_count)$p.value
  p_DI_df$DI_pval[p_DI_df$position == LOC] <- p_DI
}

We can take a look at the loci that are significantly and sufficiently imprinted (i.e. the output of final_filter from above):

cat(paste0(impr_res_FIN$position, ","))

Locus76, Locus77, Locus172, Locus173, Locus184, Locus185, Locus186,

From this set, a part is actually differentially imprinted in case samples, which is indicated by the p-value in the DI_pval column in the p_DI_df dataframe. We can control loss-of-imprinting detection, for a change, at the 5% FWER level (actually feasible here due to the small number of actually imprinted loci remaining, though we’re looking at a small toy dataset here; this isn’t necessarily the case in larger experiments):

cat(paste0(p_DI_df$position[p.adjust(p_DI_df$DI_pval, method = "holm") < 0.05], ","))

Locus172, Locus173,

We can plot histograms of both the control and case allele fractions; locus 202 is obviously imprinted in controls and loses a lot of this imprinting in cases (controls are plotted using maelstRom_imprintplot to visualize imprinting results, but since an imprinting-estimation never happens on the case data - we just detect a change in heterozygosity via logistic regression - we simply make a histogram for cases instead).

HistCTRL <- maelstRom::maelstRom_imprintplot(controlList[["Locus172"]]$ref_count, 
  controlList[["Locus172"]]$var_count, 
  allelefreq = impr_res_FIN$allele.frequency[impr_res_FIN$position=="Locus172"],
  impr = impr_res_FIN$estimated.i[impr_res_FIN$position=="Locus172"],
  SE = SEmedian, inbr = Fmedian, plot_NoImpr = TRUE, SplitPeaks = FALSE) + 
  ggplot2::ggtitle("Control")

RatioCASE <- caseList[["Locus172"]]$ref_count / 
  (caseList[["Locus172"]]$ref_count + caseList[["Locus172"]]$var_count)
CASEDat <- data.frame("Ratio" = RatioCASE)
HistCASE <- ggplot2::ggplot() + ggplot2::geom_histogram(data = CASEDat, ggplot2::aes(Ratio),
  bins = 50) + ggplot2::labs(x="Reference allele fraction", y="Frequency") + 
  ggplot2::ggtitle("Case")

gridExtra::grid.arrange(HistCTRL, HistCASE, ncol=2)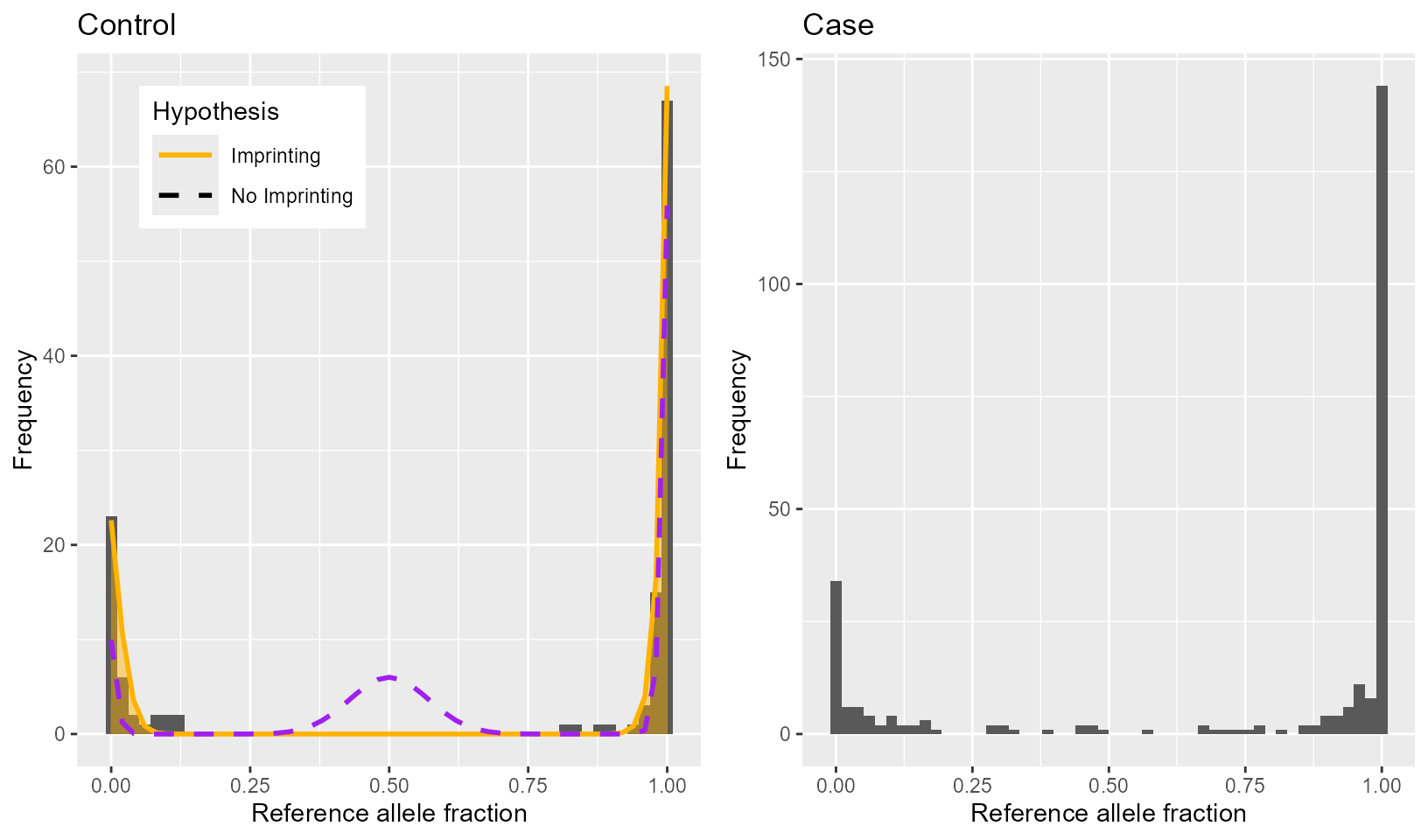

Session info

sessionInfo()
#> R version 4.3.3 (2024-02-29 ucrt)
#> Platform: x86_64-w64-mingw32/x64 (64-bit)
#> Running under: Windows 10 x64 (build 19045)
#> 
#> Matrix products: default
#> 
#> 
#> locale:
#> [1] LC_COLLATE=Dutch_Belgium.utf8 
#> [2] LC_CTYPE=Dutch_Belgium.utf8   
#> [3] LC_MONETARY=Dutch_Belgium.utf8
#> [4] LC_NUMERIC=C                  
#> [5] LC_TIME=Dutch_Belgium.utf8    
#> 
#> time zone: Europe/Brussels
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats    
#> [2] graphics 
#> [3] grDevices
#> [4] utils    
#> [5] datasets 
#> [6] methods  
#> [7] base     
#> 
#> loaded via a namespace (and not attached):
#>  [1] gmp_0.7-5          
#>  [2] sass_0.4.9         
#>  [3] utf8_1.2.4         
#>  [4] generics_0.1.3     
#>  [5] gtools_3.9.5       
#>  [6] stringi_1.8.3      
#>  [7] lattice_0.22-5     
#>  [8] digest_0.6.35      
#>  [9] magrittr_2.0.3     
#> [10] evaluate_0.24.0    
#> [11] grid_4.3.3         
#> [12] fastmap_1.2.0      
#> [13] jsonlite_1.8.8     
#> [14] ggnewscale_0.5.0   
#> [15] gridExtra_2.3      
#> [16] purrr_1.0.2        
#> [17] fansi_1.0.6        
#> [18] scales_1.3.0       
#> [19] numDeriv_2016.8-1.1
#> [20] textshaping_0.4.0  
#> [21] jquerylib_0.1.4    
#> [22] Rdpack_2.6.1       
#> [23] cli_3.6.2          
#> [24] rlang_1.1.3        
#> [25] rbibutils_2.2.16   
#> [26] munsell_0.5.1      
#> [27] withr_3.0.0        
#> [28] cachem_1.1.0       
#> [29] yaml_2.3.9         
#> [30] tools_4.3.3        
#> [31] parallel_4.3.3     
#> [32] memoise_2.0.1      
#> [33] dplyr_1.1.4        
#> [34] colorspace_2.1-0   
#> [35] ggplot2_3.5.1      
#> [36] maelstRom_1.1.11   
#> [37] hash_2.2.6.3       
#> [38] vctrs_0.6.5        
#> [39] R6_2.5.1           
#> [40] zoo_1.8-12         
#> [41] lifecycle_1.0.4    
#> [42] stringr_1.5.1      
#> [43] fs_1.6.4           
#> [44] htmlwidgets_1.6.4  
#> [45] MASS_7.3-60.0.1    
#> [46] ragg_1.3.2         
#> [47] pkgconfig_2.0.3    
#> [48] desc_1.4.3         
#> [49] pkgdown_2.0.9      
#> [50] pillar_1.9.0       
#> [51] bslib_0.7.0        
#> [52] gtable_0.3.5       
#> [53] data.table_1.16.0  
#> [54] glue_1.7.0         
#> [55] Rcpp_1.0.12        
#> [56] systemfonts_1.1.0  
#> [57] highr_0.11         
#> [58] xfun_0.45          
#> [59] tibble_3.2.1       
#> [60] tidyselect_1.2.1   
#> [61] rstudioapi_0.16.0  
#> [62] knitr_1.48         
#> [63] farver_2.1.2       
#> [64] htmltools_0.5.8    
#> [65] patchwork_1.2.0    
#> [66] labeling_0.4.3     
#> [67] rmarkdown_2.27     
#> [68] compiler_4.3.3     
#> [69] alabama_2023.1.0

References

Goovaerts, Tine, Sandra Steyaert, Chari A Vandenbussche, Jeroen Galle, Olivier Thas, Wim Van Criekinge, and Tim De Meyer. 2018. “A Comprehensive Overview of Genomic Imprinting in Breast and Its Deregulation in Cancer.” Nature Communications 9 (1): 1–14.