maelstRom Allelic Dispersion tutorial

maelstRom: Modeller of Allele-Specific Transcriptomics

Welcome to the tutorial vignette of the Modeller of Allele-Specific Transcriptomics, maelstRom! This R package offers extensive likelihood-based modelling of Allele-Specific Expression (ASE) phenomena, which includes statistical tests for their detection (e.g. genome-wide cis-eqtl mapping) or differential occurrence (e.g. copy-number alterations and/or hypermethylated loci in diseases such as cancer). All of these functionalities rely solely on regular RNAseq data, without the requirement of additional experiments such as genotyping, nor specialized data-types such as paired RNAseq.

This vignette is a step-by-step guide for a basic ASE-analysis using maelstRom starting from raw allelic counts, from input pre-processing up until vizualization of final results. For instructions on installing maelstRom, please consult maelstRom’s github home page at https://biobix.github.io/maelstRom/.

A toy dataset

maelstRom relies on per-locus per-sample nucleotide counts (A/T/C/G), relying on single-nucleotide polymorphisms (SNPs) to differentiate between alleles. Such counts are easily obtained from RNAseq BAM or SAM files, either by custom scripting or extisting functionalities such as SAMtool’s mpileup, or GATK’s CollectAllelicCounts (https://gatk.broadinstitute.org/hc/en-us/articles/360037594071-CollectAllelicCounts); the latter already filters these nucleotide counts down to just one reference- and variant-allele.

A toy data example of such input data is included in maelstRom, and is used throughout the remainder of this vignette. This toy data consists of both a hypothetical control (healthy) and case (diseased) dataset:

library(maelstRom)
#> Package 'maelstRom' version 1.1.11

data("maelstRom", package = "maelstRom")
knitr::kable(head(ControlCountsToy))

	Gene	Locus	Sample	ref_alleles	A	C	G
5295	Gene1	Locus1	Sample1	G/A/C	63	0	74
5296	Gene1	Locus1	Sample2	G/A/C	214	0	0
5297	Gene1	Locus1	Sample3	G/A/C	249	0	0
5298	Gene1	Locus1	Sample4	G/A/C	54	0	62
5299	Gene1	Locus1	Sample5	G/A/C	80	0	87
5300	Gene1	Locus1	Sample6	G/A/C	57	1	41

knitr::kable(head(CaseCountsToy))

	Gene	Locus	Sample	ref_alleles	A	T	G
11070	Gene1	Locus1	Sample129	G/A/C	194	0	321
11071	Gene1	Locus1	Sample130	G/A/C	74	0	62
11072	Gene1	Locus1	Sample131	G/A/C	62	0	49
11073	Gene1	Locus1	Sample132	G/A/C	333	0	1
11074	Gene1	Locus1	Sample133	G/A/C	226	1	137
11075	Gene1	Locus1	Sample134	G/A/C	171	0	0

This toy data contains nucleotide counts spanning 200 SNP loci across 71 genes (a gene can contain multiple SNP loci), covered by 128 control- and 268 case-samples:

length(unique(ControlCountsToy$Gene))

[1] 71

length(unique(ControlCountsToy$Locus))

[1] 200

length(unique(ControlCountsToy$Sample))

[1] 128

length(unique(CaseCountsToy$Sample))

[1] 268

Input pre-processing

The nucleotide counts above are formated as one giant dataframe. In order to use them as a maelstRom input, these need to be split into a list of seperate dataframes per locus, as maelstRoms models ASE on a per-locus level. In general, every maelstRom function has its own help page detailing the expected format of its input.

# maelstRom expects lists:
controlList <- list() 
caseList <- list()

for(LOC in unique(ControlCountsToy$Locus)){                 # For every locus...
  interDF <- ControlCountsToy[ControlCountsToy$Locus==LOC,] # extract nucleotide counts,
  controlList[[LOC]] <- interDF                             # and put it into the list
}

for(LOC in unique(CaseCountsToy$Locus)){                    # Do the same for case data
  interDF <- CaseCountsToy[CaseCountsToy$Locus==LOC,]
  caseList[[LOC]] <- interDF
}

Determine one reference and one variant allele

maelstRom’s models are built on the beta-binomial distrubution. As the name implies, this distribution models repeated observations of a binary outcome and is thus limited to two possible alleles per locus. While this may seem overly restrictive, it’s rather commonplace for SNPs in human populations to exhibit, at most, two commonly occurring SNP variants. But in the case that three or even four SNP variants should be considered, pairwise maelstRom fits of said variants are an option; beta-multinomial models, which could model all possible variants at once, are not a feature of the current version of maelstRom due to their limited added value in practical research comparative to the complexity of their implementation.

standard_alleles() takes our list of per-locus dataframes as an input, and picks the most- and second-most occurring nucleotide (at population-level) as reference- and variant nucleotide respectively, adding the resulting choice and the corresponding reference- and variant-count to each individual dataframe. If a “ref_allele” column is provided in these dataframes (as is the case for our toy data), standard_alleles() will only consider the nucleotides listed therein as possible reference- or variant candidates. This can be used to e.g. integrate expert knowledge about the current population (it is known only the listed nucleotides should occur at a certain location, and anything else is some sort of artefact), or limit all further analyses to certain alleles of particular interest.

for(n in names(controlList)){
  controlList[[n]] <- maelstRom::standard_alleles(controlList[[n]])
}
knitr::kable(head(controlList[["Locus10"]]))

	Gene	Locus	Sample	ref_alleles	A	T	C	G	ref	var	ref_count	var_count
6254	Gene4	Locus10	Sample1	C/T	0	113	176	1	C	T	176	113
6255	Gene4	Locus10	Sample2	C/T	4	0	630	1	C	T	630	0
6256	Gene4	Locus10	Sample3	C/T	0	202	273	3	C	T	273	202
6257	Gene4	Locus10	Sample4	C/T	0	0	381	1	C	T	381	0
6258	Gene4	Locus10	Sample5	C/T	0	0	683	0	C	T	683	0
6259	Gene4	Locus10	Sample6	C/T	0	0	418	2	C	T	418	0

While standard_alleles() could be run seperately on the case data, it makes sense (from both a data-analytical and biological viewpoint) to pick the same reference- and variant nucleotide as the control data:

for(n in names(caseList)){
  
  interDF <- caseList[[n]]
  interDF$ref_alleles <- controlList[[n]]$ref_alleles[1]
  interDF$ref <- controlList[[n]]$ref[1]
  interDF$var <- controlList[[n]]$var[1]
  interDF$ref_count <- interDF[,which(colnames(interDF)==interDF$ref[1])]
  interDF$var_count <- interDF[,which(colnames(interDF)==interDF$var[1])]
  
  caseList[[n]] <- interDF
  
}

knitr::kable(head(caseList[["Locus10"]]))

	Gene	Locus	Sample	ref_alleles	T	C	G	ref	var	ref_count	var_count
13114	Gene4	Locus10	Sample129	C/T	4	457	0	C	T	457	4
13115	Gene4	Locus10	Sample130	C/T	0	382	0	C	T	382	0
13116	Gene4	Locus10	Sample131	C/T	111	177	0	C	T	177	111
13117	Gene4	Locus10	Sample132	C/T	0	547	0	C	T	547	0
13118	Gene4	Locus10	Sample133	C/T	1	332	1	C	T	332	1
13119	Gene4	Locus10	Sample134	C/T	33	88	0	C	T	88	33

Prior filtering

Some rudimentary prior filtering is always worth considering, as it avoids wasting time on trying to fit models on inherently low-quality data. maelstRom’s prior_filter() provides various filtering options (see its help page; minimal median coverage across a locus, minimal number of samples, minimal minor allele count frequency i.e. the % abundance of the variant allele over all RNAseq counts, etc.). For this tutorial, we use a mild prior filter, simply requiring at least 20 control samples for a locus to be retained. We perform no prior filtering on the case data itself, but do remove loci that were removed in the control-data, as the main use of the case-data is differential ASE when compared to controls.

This 20-control-sample requirement removes 5 loci, corresponding to two genes, from the toy dataset:

for(n in names(controlList)){
  controlList[[n]] <- maelstRom::prior_filter(controlList[[n]], min_median_cov = 0, 
    min_nr_samples = 20, checkref_filter = FALSE, prior_allelefreq_filter = FALSE, 
    min_PriorAlleleFreq = 0)
  if(is.null(controlList[[n]])){
    # Filter out case data if corresponding control data was removed:
    caseList[[n]] <- NULL 
  }
}

# These loci were filtered out:
cat(paste0(setdiff(unique(ControlCountsToy$Locus), names(controlList)), ","))

Locus30, Locus31, Locus187, Locus188, Locus189,

Enabling parallellization

maelstRom can run for quite some time on larger datasets (especially when applied genome-wide), so this tutorial illustrates (optional) parallelization using R’s parallel package. This package allows the use of multiple cores for maelstRom’s computations, at least on Linux (on e.g. a local windows installation, it only allows for one core). While the number of cores NC is kept to 1 in the code below, picking a higher number should allow for a proportionate speed-up.

The following code chunk splits maelstRom’s input into a list of NC elements, which is required for parallelization using the parallel package.

NC <- 1 # Number of Cores, CHANGE THIS for a speed-up when working on a linux machine

NS <- length(controlList) 
spl <- c(0, cumsum(rep(floor(NS/NC),NC)+c(rep(1,NS-floor(NS/NC)*NC),
         rep(0,NC-NS+floor(NS/NC)*NC)))) 
ParCTRL <- vector(mode = "list", length=NC)
for(i in 1:NC){ # Put the split input data into a list for parallellisation
  ParCTRL[[i]] <- controlList[(spl[i]+1):(spl[i+1])]
}
ParCASE <- vector(mode = "list", length=NC)
for(i in 1:NC){ # Put the split input data into a list for parallellisation
  ParCASE[[i]] <- caseList[(spl[i]+1):(spl[i+1])]
}

Metaparameter estimation

maelstRom’s ASE models rely on two population-wide (constant) metaparameters: the inbreeding coefficient F of the population under study, and the sequencing error rate SE controlling the occurrence “faulty” nuceotide counts in homozygous individuals (i.e. counts of the allele for which they are not homozygous). These can very well be set at values based on expert knowledge (e.g. most natural populations should be approcimately panmictic, i.e. exhibit an inbreeding coefficient of zero) and/or the used sequencing technogy’s and alignment algorithm’s propensity to report faulty nucleotides.

Nevertheless, maelstRom has a functionality to quickly and robustly estimate these parameters from the supplied data, which can be used in the abscence of prior knowledge or, even should it be available, is a safe option anyway (as both a sanity check, or to incorporate error sources and data biases which were possibly overlooked in a would-be prior estimate). This happens by fitting the following extremely basic binomial mixture model on the supplied control data:

\[ \small \begin{aligned} \mathrm{PMF}(counts_{ref}|counts_{total}) = &\ \phi_{rr} * {\tt pbinom}(x=counts_{ref} \ |\ n=counts_{total}, p=1-SE) \ + \\ &\ \phi_{rv} * {\tt pbinom}(x=counts_{ref} \ |\ n=counts_{total}, p=0.5) \ + \\ &\ \phi_{vv} * {\tt pbinom}(x=counts_{ref} \ |\ n=counts_{total}, p=SE) \\ \end{aligned} \]

With \((\phi_{rr}, \phi_{rv}, \phi_{vv})\) to-be-fitted genotype frequencies from which the inbreeding coefficient can be estimated, and SE the sequencing error rate estimate. This model does not incorporate any ASE at all (perfectly 50-50 allelic expression in the heterozygous peak, no variance beyond technical binomial sampling variance allowed) but should be sufficient to produce robuts, median-based metaparameter estimates so long as it fits a large portion of the supplied data somewhat reasonably.

The following code chunk uses AllelicMeta_est_par() to produce the wanted estimates, and to check for the aforementioned “reasonable fit” only includes control loci with at least 20 available samples, having a median coverage of at least 4 across these samples, not returning an estimated SE over 0.035 (as this is unreasonably high and most likely indicates low-quality data or a failed model fit) and having an estimated minor allele frequency of at least 0.15 based on the above mixture model fit (anything lowes implies a rather low occurrence of at least one of the possible genotypes, and so less reliable estimates of the population’s metaparameters):

cl <- parallel::makeCluster(getOption("cl.cores", NC))
GenoFinData <- parallel::parLapply(cl, X = ParCTRL, fun = maelstRom::AllelicMeta_est_par,
  # Filter criteria mentioned in the text above:
  MinAllele_filt = 0.15, SE_filt = 0.035, NumSamp_filt = 20, MedianCov_filt = 4)
parallel::stopCluster(cl)

# Extract metaparameter estimates from the parallelly-produced output:
SE_vec <- do.call(c, lapply(GenoFinData, `[[`, 2))
F_vec <- do.call(c, lapply(GenoFinData, `[[`, 3))

SEmedian <- median(SE_vec)
Fmedian <- median(F_vec)

#estimates of resp. sequencing error rate and inbreeding coefficient:
cat(paste0(c(SEmedian, Fmedian), ","))

0.00248190279214063, 0.00872807570598289,

These metaparameter estimates seem reasonable. Please note that an extremely low sequencing error metaparameter would make fitting of homozygous peaks later down the pipeline way too strict, failing to accomodate for even a single faulty read. As such, setting SE below 0.002 is not recommended. An inbreeding coefficient close to zero is a sign of a panmictic population and commonplace when working on human data, but it could be more extreme in specialized experimental setups.

maelstRom’s ASE fit & allelic bias detection

maelstRom’s main functionality models allele-specific counts as a beta-binomial mixture of three possible genotypes. This allows for both Allelic Bias (AB), i.e. unequal allelic expression in heterozygotes, via its \(\pi\)-parameter (beta-binomial mean); and Allelic Dispersion (AD), i.e. the population-level variability in allelic expression, via its \(\theta_{het}\)-parameter (beta-binomial overdispersion):

\[ \small \begin{aligned} \mathrm{PMF}(counts_{ref}|counts_{total}) = &\ \phi_{rr} * {\tt pBetaBinom}(x=counts_{ref} \ |\ n=counts_{total}, \pi=1-SE, \theta=\theta_{hom}) \ + \\ &\ \phi_{rv} * {\tt pBetaBinom}(x=counts_{ref} \ |\ n=counts_{total}, \pi=\pi_{het}, \theta=\theta_{het}) \ + \\ &\ \phi_{vv} * {\tt pBetaBinom}(x=counts_{ref} \ |\ n=counts_{total}, \pi=SE, \theta=\theta_{hom}) \\ \end{aligned} \]

With the remaining parameters being: \((\phi_{rr}, \phi_{rv}, \phi_{vv})\) the fitted genotype frequencies, and \(\theta_{hom}\) the beta-binomial overdispersion parameter in homozygotes. By fitting the former through expectation-maximization, which iteratively assigns each sample to the three possible genotypes, then estimates all genotype-specific beta-binomial parameters, maelstRom does not require additional genotyping-data.

The code chunk below uses the EMfit_betabinom_robust function to fit this mixture model, and writes the results to ASEfit_res. Additionally, it uses the previously calculated inbreeding coefficient Fmedian to test every locus for significant deviation from Hardy-Weinberg Equilibrium (HWE), which could indicate a failed model fit and can thus be used as a goodness-of-fit filter criterion later:

ASEfitter <- function(data){
  
  positions <- names(data)
  results <- data.frame()
  
  for (z in positions) {
    maelstRomres <- maelstRom::EMfit_betabinom_robust(data_counts = data[[z]], 
                                            SE = SEmedian, inbr = Fmedian)
    
    data[[z]] <- maelstRomres$data_hash
    
    res_loc <- data.frame("Gene" = data[[z]]$Gene[1] ,"Locus" = z, 
      "reference" = data[[z]]$ref[1], "variant" = data[[z]]$var[1], 
      "phi_rr" = maelstRomres$rho_rr, "phi_rv" = maelstRomres$rho_rv, 
      "phi_vv" = maelstRomres$rho_vv, "pi" = as.numeric(maelstRomres$AB), 
      "AB_pval" = as.numeric(maelstRomres$AB_p), "theta_hom" = maelstRomres$theta_hom, 
      "theta_het" = maelstRomres$theta_het, "allele.frequency" = data[[z]]$allelefreq[1], 
      "coverage" =  median(data[[z]]$ref_count+data[[z]]$var_count),
      "nr_samples" = nrow(data[[z]]), 
      "quality" = maelstRomres$quality,
      stringsAsFactors = FALSE)
    
    results <- rbind(results, res_loc) # results; one position per line
  }
  
  results <- maelstRom::HWE_chisquared(data = data, Fmedian, results = results)
  results$HWEpval[is.na(results$HWEpval)] <- -1
  results$HWE_TestStat[is.na(results$HWE_TestStat)] <- -1
  return(list(data, results))
  
}

cl <- parallel::makeCluster(getOption("cl.cores", NC))
parallel::clusterExport(cl, c("Fmedian", "SEmedian"))
ASEfit <- parallel::parLapply(cl, X = ParCTRL, fun = ASEfitter)
parallel::stopCluster(cl)

ParCTRL <- lapply(ASEfit, `[[`, 1)
controlList <- do.call(c, lapply(ASEfit, `[[`, 1))
ASEfit_res <- do.call("rbind", lapply(ASEfit, `[[`, 2))

ASEfit_res contains all per-locus parameters of the beta-binomial mixture model discussed above. Also, besides the just mentioned results of the chi square test for deviation from HWE, it contains additional quality metrics which can be used in filtering of results, those being each locus’ reference allele frequency among genotypes in the population (allele.frequency), median count coverage (coverage), the number of samples involved in the fit (nr_samples) and lastly, a quality flag which equals “!” in the case maelstRom’s fit fails for this particular locus, which is usually due to no apparent heterozygotes being present (quality). Finally, AB_pval contains the result (raw p-value) of a likelihood ratio test for whether \(\pi_{het}\) is significantly different from 0.5, thus detecting whether there’s an Allelic Bias (AB) in expression in a given locus.

knitr::kable(head(ASEfit_res))

Gene	Locus	reference	variant	phi_rr	phi_rv	phi_vv	pi	AB_pval	theta_hom	theta_het	allele.frequency	coverage	nr_samples	HWEpval	HWE_TestStat
Gene1	Locus1	A	G	0.3904620	0.4845264	0.1250116	0.4898086	0.2898711	0.0602616	0.0173647	0.6327252	190.5	128	0.9189807	0.1689803
Gene1	Locus2	A	G	0.7031276	0.2812474	0.0156250	0.5647487	0.0000103	0.0366680	0.0130104	0.8437513	96.0	128	0.8149959	0.4091444
Gene1	Locus3	C	A	0.7031522	0.2812201	0.0156277	0.5093620	0.3614079	0.0837429	0.0066971	0.8437623	116.5	128	0.8151967	0.4086518
Gene2	Locus4	T	C	0.4163886	0.4900306	0.0935808	0.6226814	0.0000000	0.0481506	0.0202838	0.6614039	27.0	128	0.7073233	0.6925348
Gene2	Locus5	T	C	0.5469213	0.3828949	0.0701838	0.5143016	0.3560640	0.0449810	0.0180381	0.7383688	34.0	128	0.9999981	0.0000037
Gene2	Locus6	G	T	0.1370091	0.5524136	0.3105773	0.7119506	0.0000000	0.0207748	0.0159835	0.4132159	15.0	128	0.4919931	1.4185814

In addition to this dataframe of per-locus fitting results, the per-locus allelic count data in controlList has been updated to include, for every sample, its Expectation-Maximization-assigned likelihood to be originating from a reference homozygous, heterozygous, or variant homozygous individual (prr, prv, pvv), listing the most likely of these options in the “genotypeN” column.

knitr::kable(head(controlList[["Locus27"]][,c("Sample", "ref", "var", "ref_count", "var_count", 
                                           "prr", "prv", "pvv", "genotypeN")]))

	Sample	ref	var	ref_count	var_count	prr	prv	pvv	genotypeN
16915	Sample1	C	T	7	0	0.9954662	0.0045338	0.0000000	rr
16916	Sample2	C	T	2	7	0.0000025	0.9987087	0.0012888	rv
16917	Sample3	C	T	6	6	0.0000987	0.9998962	0.0000050	rv
16918	Sample4	C	T	9	0	0.9985476	0.0014524	0.0000000	rr
16919	Sample5	C	T	2	8	0.0000010	0.9980893	0.0019098	rv
16920	Sample6	C	T	3	3	0.0008466	0.9991102	0.0000432	rv

We can now list loci showcasing significant AB (i.e. deviation from \(\pi_{het} = 0.5\)), both statistically (5% FDR level) and in terms of effect size (a deviation from 0.5 of at least 0.1). The code chunk below also includes some basic quality filter criteria (a median counts coverage of at least 10 across at least 20 expected heterozygotes to actually fit AB on; with the latter calculated as the number of samples times the fraction of heterozygotes \(\phi_{rv}\)). Furthermore, to ensure a good model fit, we require no problems regarding the quality flag (i.e. not equal to “!”), a detected AB that’s not more extreme than 0.9 or 0.1, and a HWE-deviation-checking p-value of at least 0.001 (a filter criterion often used to check for HWE conformity: Sha and Zhang (2011), Teo et al. (2007), Rohlfs and Weir (2008)); any of these last three criteria not being met indicates a possibly faulty model fit.

A final, optional, filter, is throwing out loci for which either \(\pi_{het}/\theta_{het} <= 1\) OR \((1-\pi_{het})/\theta_{het} <= 1\), as any of these inequalities being met leads to stange behavior of the beta-binomial distribution (either getting its mode stuck at 0 or 1 or, if both inequalities are true, becoming bimodal). This being the case usually suggests a failed model fit as well (for an illustration, try to plot Locus172’s fit - which is normally removed by this final filter - using the plotting function in the next code chunk after the code chunk below).

# Statistical evidence for significant AB at the 5% FDR level,
# only retaining reliable (high-quality) loci with a large enough effect size:
cat(paste0(paste(ASEfit_res$Locus[
  
  p.adjust(ASEfit_res$AB_pval, method = "BH") < 0.05 &
  (abs(ASEfit_res$pi - 0.5) > 0.1) & 
  ASEfit_res$coverage >= 10 & 
  ASEfit_res$nr_samples * ASEfit_res$phi_rv >= 20  &   
  ASEfit_res$quality != "!" &
  (ASEfit_res$pi < 0.9 &  ASEfit_res$pi > 0.1) & 
  ASEfit_res$HWEpval >= 0.001 &
  ASEfit_res$pi/ASEfit_res$theta_het > 1 &
  (1-ASEfit_res$pi)/ASEfit_res$theta_het > 1], 
  
  collapse = ", "), ","))

Locus4, Locus6, Locus10, Locus45, Locus73, Locus84, Locus104, Locus114,

maelstRom’s maelstRom_EMfitplot() allows us to plot the previously obtained beta-binomial mixture model fits, together with an allele fraction histogram depicting the actual data that’s being fit. In addition to to-be-plotted data and parameters, the function requires two additional inputs.

“nbins”: the number of bins for the histogram of observed per-sample (reference) allele fractions
“ScaleCount”: the beta-binomial distribution is a discrete probability distribution that contains a parameter for the total number of observations, \(n\). The distributions being plotted as lineplots by maelstRom_EMfitplot() are beta-binomials, but with their x-axis range rescaled from 0-to-\(n\) to 0-to-1. However, even when rescaled, the shape (variance) of this distribution still depends on the underlying \(n\)-parameter being used, which is thus asked as an input argument, ScaleCount. In order to most closely fit the underlying histogram of observed data, the code chunk below uses the locus’ median coverage as ScaleCount.

maelstRom_EMfitplot() accepts a lot of other optional arguments for further plotting functionalities and customization. Additionally, it returns the plot as a ggplot object, which can be freely customized even further.

PlotData <- controlList[["Locus104"]]
PlotData_eqtl <- ASEfit_res[ASEfit_res$Locus=="Locus104",]

loc_plot <- maelstRom::maelstRom_EMfitplot(ref_counts=PlotData$ref_count, 
  var_counts=PlotData$var_count, pr=PlotData_eqtl$phi_rr, prv=PlotData_eqtl$phi_rv,
  pv=PlotData_eqtl$phi_vv, theta_hom=PlotData_eqtl$theta_hom, 
  theta_het=PlotData_eqtl$theta_het, probshift=as.numeric(PlotData_eqtl$pi), 
  SE=SEmedian, ScaleCount = PlotData_eqtl$coverage, nbins = 30)

loc_plot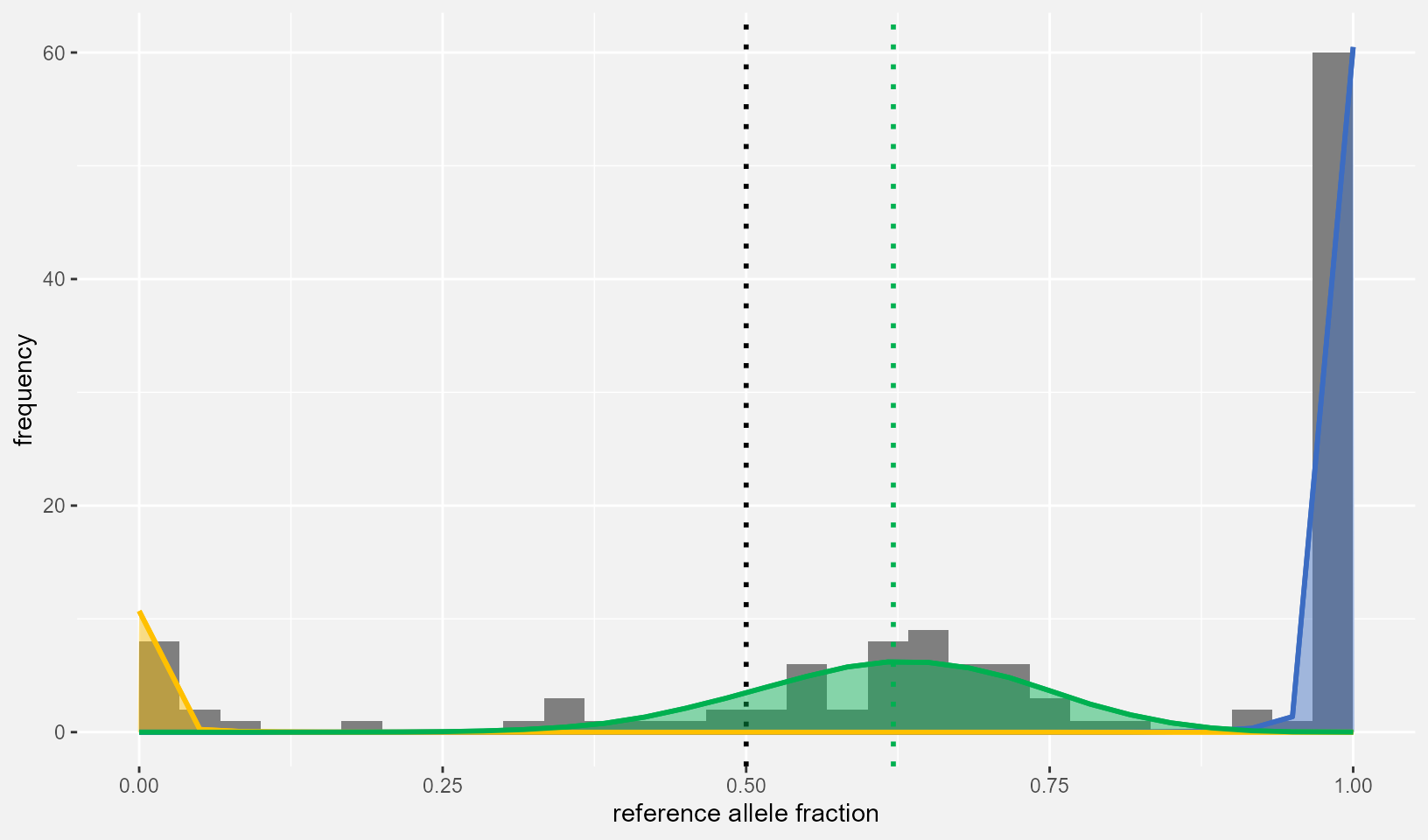

Besides the previously established statistical evidence, this plot makes it visually clear that Locus104’s heterozygotes are biased towards allelic expression of the reference allele.

Differential allelic dispersion

maelstRom hypothesizes that early (so potentially causal) case-specific dysregulation events such as copy number alterations, aberrant hypermethylation, and gene silencing (incomplete silencing; either inherent to the mechanism, and/or seemingly observed as incomplete due to e.g. tumor impurity of the allelic count data) can cause an allelic expression bias within one individual but will not, at a population-level, consistently favor the same allele. Thus, rather than causing an allelic bias (AB), this dysregulation will result in an increased variance of allelic expression; we call this variance Allelic Dispersion (AD), and its increase in e.g. disease and cancer differential Allelic Dispersion (dAD).

Detecting dAD between two populations can be done via a likelihood ratio test, comparing: (1) a model fitting ALL data, both control and case, as one beta-binomial mixture model, with (2) a model allowing the control- and case data to have their separate \(\theta_{het}\) parameters. This is done by the dAD_analysis() function below, which internally performs a number of fits:

A fit on control (OnlyC) and case (OnlyT) data separately for outlier detection.
A joint fit on control and case data sharing all parameters across both populations (H0, the null hypothesis of the dAD-test)
A fit using a separate \(\theta_{het}\) parameter for controls and cases

Besides this final and most interesting fit, the dAD_res object below contains the parameter estimations for the other three fits (OnlyC, OnlyT, H0), alongside a selection of quality metrics and a p-value testing for deviation from HWE in controls and cases (“HWEC”, “HWET”) which can be used as filter critaria.

The code chunk below only prints the most interesting results: the actual dAD-detecting pval along with and effect size (\(\theta_{het}\) in both cases and controls) and the most relevant filter critaria in controls (number of estimated heterozygotes, median coverage, and the HWE-deviation-testing p-value):

ParTOT <- vector(mode = "list", length=NC)
for(i in 1:NC){ # Put the splitted input data into a list for parallellisation
  ParTOT[[i]] <- list(ParCTRL[[i]], ParCASE[[i]])
}

cl <- parallel::makeCluster(getOption("cl.cores", NC))
dADFinData <- parallel::parLapply(cl, X = ParTOT, fun = maelstRom::dAD_analysis, 
                                  SE = SEmedian, inbr = Fmedian)
parallel::stopCluster(cl)

dAD_res <- do.call("rbind", lapply(dADFinData, `[[`, 1))
  
controlList <- do.call(c, lapply(dADFinData , `[[`, 2))
caseList <- do.call(c, lapply(dADFinData, `[[`, 3))

knitr::kable(head(dAD_res[,c("Locus", "Gene", "dAD_pval", "ThetaHetC", "ThetaHetT", 
                             "RhoC", "RhoT", "NumHetC", "CovC_Med", "HWEC")]))

Locus	Gene	dAD_pval	ThetaHetC	ThetaHetT	RhoC	RhoT	NumHetC	CovC_Med	HWEC
Locus1	Gene1	0.0145737	0.0243768	0.0515579	0.0237967	0.0490300	62.01938	190.5	0.9189807
Locus2	Gene1	0.0001449	0.0141543	0.0751320	0.0139567	0.0698817	35.99966	96.0	0.8149959
Locus3	Gene1	0.0000012	0.0073516	0.0785041	0.0072980	0.0727898	35.99617	116.5	0.8151967
Locus4	Gene2	0.3304979	0.0208067	0.0386687	0.0203826	0.0372291	62.72392	27.0	0.7073233
Locus5	Gene2	0.6137441	0.0188209	0.0262031	0.0184732	0.0255340	49.01055	34.0	0.9999981
Locus6	Gene2	0.3453054	0.0213316	0.0021231	0.0208861	0.0021186	70.70894	15.0	0.4919931

RhoC and RhoT are simple rescalings of ThetaHetC and ThetaHetT respectively:

\[ \rho = \frac{1}{(1/\theta)+1} \] which ranges from 0 to 1 instead of \(\theta\)’s 0 to infinity, and is thus more suitable for visualization purposes. The code above updated the inputs in controlList and caseList to include a column marking outliers as well, which can come in handy for future analyses.

Significant dAD loci with increased \(\theta_{het}\) in cases, and passing some basic filter criteria, can now be selected:

cat(paste0(dAD_res$Locus[
  p.adjust(dAD_res$dAD_pval, method = "BH") < 0.001 & #Significant at 0.1% FDR
    dAD_res$RhoT > dAD_res$RhoC & #Increased AD in cases
    #Median coverage of at least 10 in both cases and controls:
    dAD_res$CovC_Med >= 10 & dAD_res$CovT_Med >= 10 & 
    #Number of heterozygotes and HWE-conformity are only checked in controls,
    #as case-data can be rather erratic, e.g. due to tumorigenesis
    dAD_res$NumHetC >= 15 & dAD_res$HWEC >= 0.001
  ], ","))

Locus3, Locus18, Locus19, Locus20, Locus69, Locus72, Locus74, Locus75, Locus116, Locus117, Locus118, Locus138, Locus141, Locus142, Locus143, Locus147, Locus148, Locus149, Locus154, Locus159, Locus160, Locus161, Locus164, Locus165, Locus170,

As before, maelstRom_EMfitplot can be used to visualize the control-case AD difference in these loci:

CTRL_DF <- controlList[["Locus19"]]
CASE_DF <- caseList[["Locus19"]]
PlotData_dAD <- dAD_res[dAD_res$Locus=="Locus19",]

dAD_plot1 <- maelstRom::maelstRom_EMfitplot(ref_counts=CTRL_DF$ref_count, var_counts=CTRL_DF$var_count,
  pr=PlotData_dAD$phi_rr, prv=PlotData_dAD$phi_rv, pv=PlotData_dAD$phi_vv, 
  theta_hom = PlotData_dAD$ThetaHom, theta_het = PlotData_dAD$ThetaHetC, 
  probshift = PlotData_dAD$Pi, SE=SEmedian, ScaleCount = PlotData_dAD$CovC_Med, nbins = 30)

dAD_plot2 <- maelstRom::maelstRom_EMfitplot(ref_counts=CASE_DF$ref_count, var_counts=CASE_DF$var_count,
  pr=PlotData_dAD$phi_rr, prv=PlotData_dAD$phi_rv, pv=PlotData_dAD$phi_vv, 
  theta_hom = PlotData_dAD$ThetaHom, theta_het = PlotData_dAD$ThetaHetT, 
  probshift = PlotData_dAD$Pi, SE=SEmedian, ScaleCount = PlotData_dAD$CovT_Med, nbins = 30)

gridExtra::grid.arrange(dAD_plot1, dAD_plot2, ncol=2)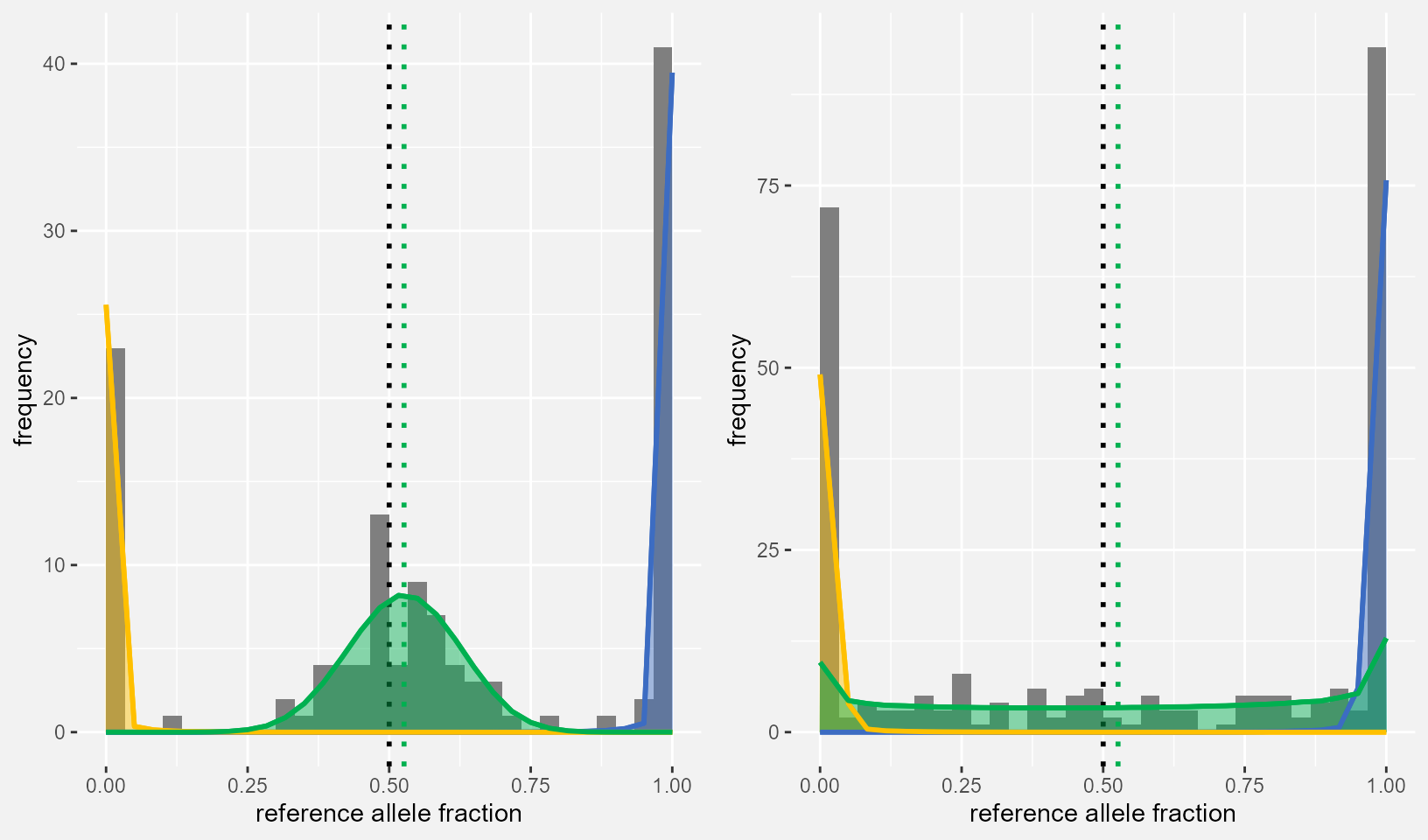

Combining locus-level results to gene-level results.

While locus-level results can be informative by themselves, it is - for biological interpretation - easier to have results (\(\theta\) or \(\rho\) values, p-values) at the gene-level. Post-hoc p-value combination (so without directly modelling counts at the transcript- or gene-level) is especially tricky: the well-established Fisher combination method is only valid when combining independent tests (and independency is hard to argue for SNPs that are close enough to have their count data originate from the same RNA molecule or RNAseq read) while other combination methods like Cauchy combination (Liu and Xie (2020)) behave like a generalized mean - in the sense that the resulting p-value will never be lower than the minimal supplied p-value and, as such, is unable to combine statistical evidence from two tests into an even more significant p-value.

To this end, maelstRom implements a correlation-corrected Lancaster p-value combination (the Lancaster combination being, itself, a weighted version of the Fischer combination), as published by Dai, Leeder, and Cui (2014), and further optimized by implementation of the Score test (instead of the likelihood ratio test) during the sample-label-permutation-based correlation calculation (which avoids iterative re-fitting of maelstRom’s beta-binomial mixture model, as the score test relies solely on the H0 model fit, which is constant across sample-label permutations).

The previously mentioned (combined) p-values (Fisher, Cauchy, Lancaster, correlation-corrected Lancaster) are calculated in the code chunk below, by maelstRom’s AdvancedPvalcomb function which, besides the sequencing error SE, also takes the number of permutations to use during correlation-correction nperm as an input; the higher this number, the longer the code runs. Dai, Leeder, and Cui (2014) uses 1000 permutations in their publication so we do the same here:

# Split results across cores for parallellization in a gene-wise manner
goi <- unique(dAD_res$Gene)
NS <- length(goi)
spl <- c(0, cumsum(rep(floor(NS/NC),NC)+c(rep(1,NS-floor(NS/NC)*NC),
              rep(0,NC-NS+floor(NS/NC)*NC)))) # Helps in splitting input data
inputlist <- vector(mode = "list", length=NC)

for(j in 1:NC){ # Put the splitted input data into a list for parallellisation
  GenesNow <- goi[(spl[j]+1):(spl[j+1])]
  ResDF_OIs <- ControlOIs <- CaseOIs <- vector(mode = "list", length = length(GenesNow))
  for(k in 1:length(GenesNow)){
    ResDF_OIs[[k]] <- dAD_res[dAD_res$Gene == GenesNow[k],]
    LocsOI <- ResDF_OIs[[k]]$Locus
    ControlOIs[[k]] <- (controlList)[LocsOI]
    CaseOIs[[k]] <- (caseList)[LocsOI]
  }
  inputlist[[j]] <- list(GenesNow, ResDF_OIs, ControlOIs, CaseOIs)
}

# Call the AdvancedPvalcomb function
cl <- parallel::makeCluster(getOption("cl.cores", NC))
AdvPVALs <- parallel::parLapply(cl, X = inputlist, fun = maelstRom::AdvancedPvalcomb, SE = SEmedian, nperm = 1000)
parallel::stopCluster(cl)

# Extract gene-level p-values
FisherPVAL_vec <- LancasterPVAL_vec <-  CorLancasterPVAL_vec <-  CauchyPVAL_vec <- c()
for(ii in 1:NC){
  FisherPVAL_vec <- c(FisherPVAL_vec, AdvPVALs[[ii]][[1]])
  LancasterPVAL_vec <- c(LancasterPVAL_vec, AdvPVALs[[ii]][[2]]) 
  CorLancasterPVAL_vec <- c(CorLancasterPVAL_vec, AdvPVALs[[ii]][[3]])
  CauchyPVAL_vec <- c(CauchyPVAL_vec, AdvPVALs[[ii]][[4]])
}

There are a number of genes with highly correlated SNP-level allelic counts (suggesting said SNP are located in close proximity to eachother on the genome or on (processed) transcripts from which RNAseq data is generated), for which the correlation-corrected Lancaster p-value was greatly reduced when compared to the (non-corrected) Lancaster p-value:

cat(paste0(LancasterPVAL_vec[c(23, 40, 51)], ","))

3.67073174475383e-12, 3.22181819373512e-41, 1.42550478480222e-28,

cat(paste0(CorLancasterPVAL_vec[c(23, 40, 51)], ","))

8.58344380865356e-07, 8.20920695441837e-20, 1.06076319143304e-11,

Most genes, however, consist of more independent SNP-level data (notice the relatively small change):

cat(paste0(LancasterPVAL_vec[1:5], ","))

2.63624315913471e-09, 0.517344906897836, 4.12379217454491e-06, 0.000739519269403496, 0.8312901339832,

cat(paste0(CorLancasterPVAL_vec[1:5], ","))

1.68611148785551e-07, 0.517344906897836, 5.17436630368803e-06, 0.000739519269403496, 0.826412966371467,

Next to the per-gene correlation-corrected Lancaster p-value, we can add averages of its per-SNP \(\rho_{control}\)s and \(\rho_{case}\)s (weighted averages, according to each SNP’s \(\sqrt{median\ coverage \times estimated\ number\ of\ heterozygotes}\) in controls or cases respectively), as well as some (weighted averages of) quality metrics:


dAD_res_Gene <- data.frame(Gene=goi, Nr_SNPs=rep(NA,length(goi)), 
  Mean_RhoC=rep(NA,length(goi)), Mean_RhoT=rep(NA,length(goi)), CorLancasterPVAL = CorLancasterPVAL_vec, 
  Mean_NumHetC=rep(NA,length(goi)), Mean_NumHetT=rep(NA,length(goi)), Mean_CovC_Med=rep(NA,length(goi)), Mean_CovT_Med=rep(NA,length(goi)), 
  stringsAsFactors = F)     

for(Gene in goi){
  
  dAD_res_Gene$Nr_SNPs[dAD_res_Gene$Gene == Gene] <- sum(dAD_res$Gene == Gene)

  CovC_Meds <- dAD_res$CovC_Med[dAD_res$Gene == Gene]
  CovT_Meds <- dAD_res$CovT_Med[dAD_res$Gene == Gene]
  NumHetCs <- dAD_res$NumHetC[dAD_res$Gene == Gene]
  NumHetTs <- dAD_res$NumHetT[dAD_res$Gene == Gene]
  Cweights <- Tweights <- c()
  for(i in 1:length(CovC_Meds)){
    Cweights <- c(Cweights, sqrt(CovC_Meds[i]*NumHetCs[i]))
    Tweights <- c(Tweights, sqrt(CovT_Meds[i]*NumHetTs[i]))
  }
  
  dAD_res_Gene$Mean_NumHetC[dAD_res_Gene$Gene == Gene] <- maelstRom::combine_p_gene(NumHetCs, weights = 
                                                            sqrt(CovC_Meds), method = "arithmetic")
  dAD_res_Gene$Mean_NumHetT[dAD_res_Gene$Gene == Gene] <- maelstRom::combine_p_gene(NumHetTs, weights = 
                                                            sqrt(CovT_Meds), method = "arithmetic")
  dAD_res_Gene$Mean_CovC_Med[dAD_res_Gene$Gene == Gene] <- maelstRom::combine_p_gene(CovC_Meds, weights = 
                                                            sqrt(NumHetCs), method = "arithmetic")
  dAD_res_Gene$Mean_CovT_Med[dAD_res_Gene$Gene == Gene] <- maelstRom::combine_p_gene(CovT_Meds, weights = 
                                                            sqrt(NumHetTs), method = "arithmetic")
  dAD_res_Gene$Mean_RhoC[dAD_res_Gene$Gene == Gene] <- maelstRom::combine_p_gene(dAD_res$RhoC[dAD_res$Gene == 
                                                        Gene], weights = Cweights, method = "arithmetic")
  dAD_res_Gene$Mean_RhoT[dAD_res_Gene$Gene == Gene] <- maelstRom::combine_p_gene(dAD_res$RhoT[dAD_res$Gene == 
                                                        Gene], weights = Tweights, method = "arithmetic")
}

knitr::kable(head(dAD_res_Gene))

Gene	Nr_SNPs	Mean_RhoC	Mean_RhoT	CorLancasterPVAL	Mean_NumHetC	Mean_NumHetT	Mean_CovC_Med	Mean_CovT_Med
Gene1	3	0.0167054	0.0609712	0.0000002	46.44028	87.74274	139.63312	173.500947
Gene2	3	0.0198453	0.0243574	0.5173449	59.43292	114.12708	24.77530	18.029318
Gene3	3	0.0118674	0.0307354	0.0000052	62.15882	116.28909	169.44331	124.286181
Gene4	2	0.0218546	0.0301046	0.0007395	37.13462	99.43332	240.21210	187.994362
Gene5	3	0.0142337	0.0136280	0.8264130	42.79365	93.49767	10.53696	8.449295
Gene6	3	0.0296196	0.0379265	0.2284072	36.47197	67.56134	16.07402	15.540588

Using similar criteria as for the SNP-level results, we can now filter out those genes showing the most significant dAD:

cat(paste0(paste(dAD_res_Gene$Gene[
  p.adjust(dAD_res_Gene$CorLancasterPVAL, method = "BH") < 0.001 & #Significant at 0.1% FDR
    dAD_res_Gene$Mean_RhoT > dAD_res_Gene$Mean_RhoC & #Increased AD in cases
    dAD_res_Gene$Mean_CovC_Med >= 10 & dAD_res_Gene$Mean_CovT_Med >= 10 & 
    dAD_res_Gene$Mean_NumHetC >= 15
  ], collapse = ", "), ","))

Gene1, Gene3, Gene7, Gene24, Gene25, Gene26, Gene41, Gene49, Gene50, Gene52, Gene56, Gene58, Gene60,

GeneToPlot <- "Gene7"
LocsToPlot <- dAD_res$Locus[dAD_res$Gene==GeneToPlot]

PlotList <- list()
t <- 0

for(LTP in LocsToPlot){
  t <- t+1
  CTRL_DF <- controlList[[LTP]]
  CASE_DF <- caseList[[LTP]]
  PlotData_dAD <- dAD_res[dAD_res$Locus==LTP,]
  
  PlotList[[t]] <- maelstRom::maelstRom_EMfitplot(ref_counts=CTRL_DF$ref_count, var_counts=CTRL_DF$var_count,
  pr=PlotData_dAD$phi_rr, prv=PlotData_dAD$phi_rv, pv=PlotData_dAD$phi_vv, 
  theta_hom = PlotData_dAD$ThetaHom, theta_het = PlotData_dAD$ThetaHetC, 
  probshift = PlotData_dAD$Pi, SE=SEmedian, ScaleCount = PlotData_dAD$CovC_Med, nbins = 30)
  
  t <- t+1
  PlotList[[t]] <- maelstRom::maelstRom_EMfitplot(ref_counts=CASE_DF$ref_count, var_counts=CASE_DF$var_count,
  pr=PlotData_dAD$phi_rr, prv=PlotData_dAD$phi_rv, pv=PlotData_dAD$phi_vv, 
  theta_hom = PlotData_dAD$ThetaHom, theta_het = PlotData_dAD$ThetaHetT, 
  probshift = PlotData_dAD$Pi, SE=SEmedian, ScaleCount = PlotData_dAD$CovT_Med, nbins = 30)
}

gridExtra::grid.arrange(grobs = PlotList, ncol=2)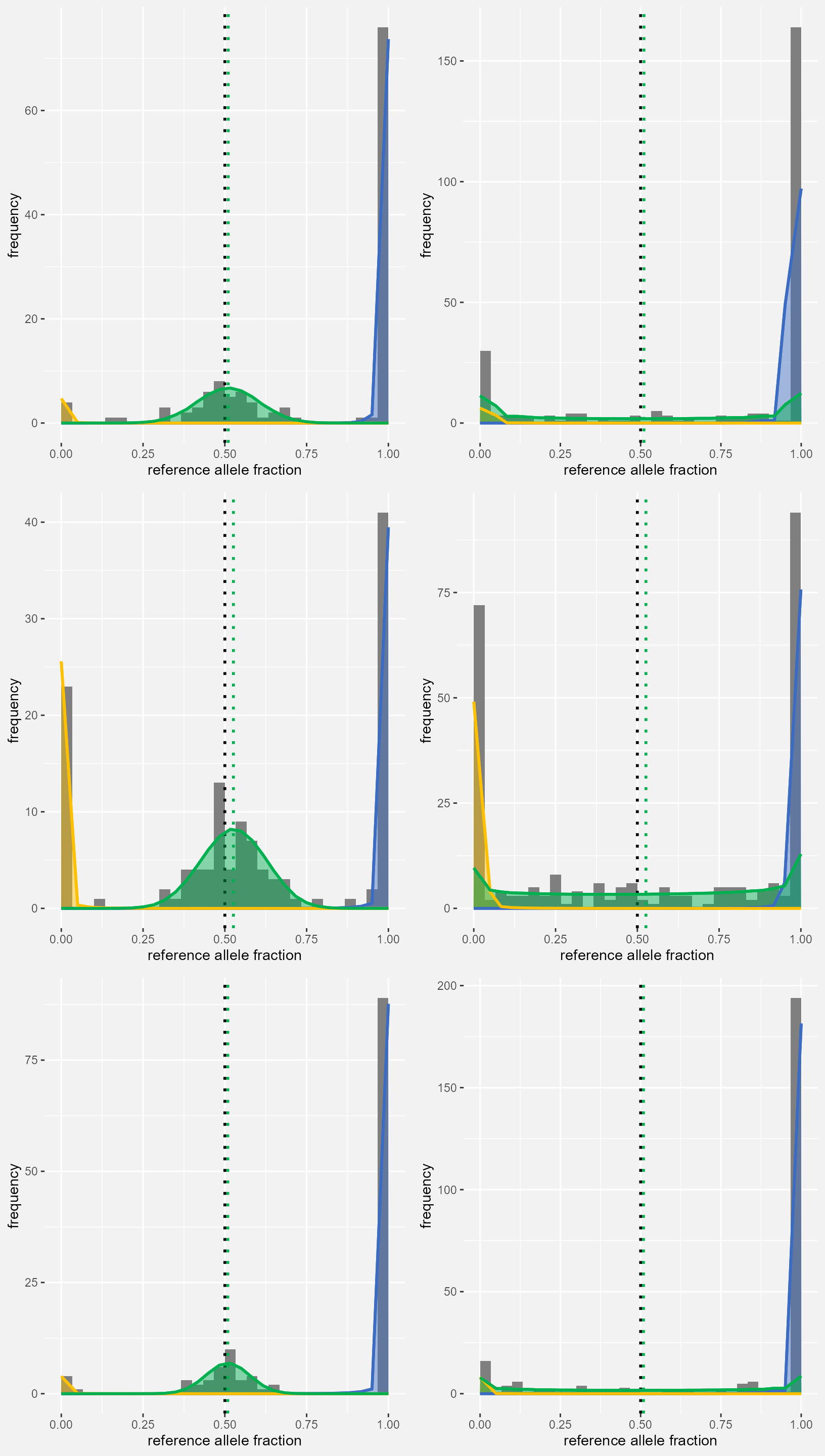

Session info

sessionInfo()
#> R version 4.3.3 (2024-02-29 ucrt)
#> Platform: x86_64-w64-mingw32/x64 (64-bit)
#> Running under: Windows 10 x64 (build 19045)
#> 
#> Matrix products: default
#> 
#> 
#> locale:
#> [1] LC_COLLATE=Dutch_Belgium.utf8 
#> [2] LC_CTYPE=Dutch_Belgium.utf8   
#> [3] LC_MONETARY=Dutch_Belgium.utf8
#> [4] LC_NUMERIC=C                  
#> [5] LC_TIME=Dutch_Belgium.utf8    
#> 
#> time zone: Europe/Brussels
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats    
#> [2] graphics 
#> [3] grDevices
#> [4] utils    
#> [5] datasets 
#> [6] methods  
#> [7] base     
#> 
#> other attached packages:
#> [1] maelstRom_1.1.11
#> 
#> loaded via a namespace (and not attached):
#>  [1] gmp_0.7-5          
#>  [2] sass_0.4.9         
#>  [3] utf8_1.2.4         
#>  [4] generics_0.1.3     
#>  [5] gtools_3.9.5       
#>  [6] stringi_1.8.3      
#>  [7] lattice_0.22-5     
#>  [8] digest_0.6.35      
#>  [9] magrittr_2.0.3     
#> [10] evaluate_0.24.0    
#> [11] grid_4.3.3         
#> [12] fastmap_1.2.0      
#> [13] jsonlite_1.8.8     
#> [14] ggnewscale_0.5.0   
#> [15] gridExtra_2.3      
#> [16] purrr_1.0.2        
#> [17] fansi_1.0.6        
#> [18] scales_1.3.0       
#> [19] numDeriv_2016.8-1.1
#> [20] textshaping_0.4.0  
#> [21] jquerylib_0.1.4    
#> [22] Rdpack_2.6.1       
#> [23] cli_3.6.2          
#> [24] rlang_1.1.3        
#> [25] rbibutils_2.2.16   
#> [26] munsell_0.5.1      
#> [27] withr_3.0.0        
#> [28] MAGE_1.0.0.18      
#> [29] cachem_1.1.0       
#> [30] yaml_2.3.9         
#> [31] tools_4.3.3        
#> [32] parallel_4.3.3     
#> [33] memoise_2.0.1      
#> [34] dplyr_1.1.4        
#> [35] colorspace_2.1-0   
#> [36] ggplot2_3.5.1      
#> [37] hash_2.2.6.3       
#> [38] vctrs_0.6.5        
#> [39] R6_2.5.1           
#> [40] zoo_1.8-12         
#> [41] lifecycle_1.0.4    
#> [42] stringr_1.5.1      
#> [43] fs_1.6.4           
#> [44] htmlwidgets_1.6.4  
#> [45] MASS_7.3-60.0.1    
#> [46] ragg_1.3.2         
#> [47] pkgconfig_2.0.3    
#> [48] desc_1.4.3         
#> [49] pkgdown_2.0.9      
#> [50] pillar_1.9.0       
#> [51] bslib_0.7.0        
#> [52] gtable_0.3.5       
#> [53] data.table_1.16.0  
#> [54] glue_1.7.0         
#> [55] Rcpp_1.0.12        
#> [56] systemfonts_1.1.0  
#> [57] highr_0.11         
#> [58] xfun_0.45          
#> [59] tibble_3.2.1       
#> [60] tidyselect_1.2.1   
#> [61] rstudioapi_0.16.0  
#> [62] knitr_1.48         
#> [63] farver_2.1.2       
#> [64] htmltools_0.5.8    
#> [65] patchwork_1.2.0    
#> [66] labeling_0.4.3     
#> [67] rmarkdown_2.27     
#> [68] compiler_4.3.3     
#> [69] alabama_2023.1.0

References

Dai, Hongying, J Steven Leeder, and Yuehua Cui. 2014. “A Modified Generalized Fisher Method for Combining Probabilities from Dependent Tests.” Frontiers in Genetics 5: 32.

Liu, Yaowu, and Jun Xie. 2020. “Cauchy Combination Test: A Powerful Test with Analytic p-Value Calculation Under Arbitrary Dependency Structures.” Journal of the American Statistical Association 115 (529): 393–402.

Rohlfs, Rori V, and Bruce S Weir. 2008. “Distributions of Hardy–Weinberg Equilibrium Test Statistics.” Genetics 180 (3): 1609–16.

Sha, Qiuying, and Shuanglin Zhang. 2011. “A Test of Hardy-Weinberg Equilibrium in Structured Populations.” Genetic Epidemiology 35 (7): 671–78.

Teo, Yik Y, Andrew E Fry, Taane G Clark, ES Tai, and Mark Seielstad. 2007. “On the Usage of HWE for Identifying Genotyping Errors.” Annals of Human Genetics 71 (5): 701–3.

Cedric Stroobandt

2024-11-27